Answer:
A) increasing by 9% each year
B) Account B
Explanation:
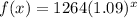
Part A
The amount of money in account A is increasing by 9% each year.
General form of an exponential function:
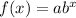
 is the initial value,
is the initial value,
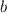 is the growth factor and
is the growth factor and
 is time.
is time.
- If b < 1 then the function is decreasing
- If b > 1 then the function is increasing
As b = 1.09 > 1 then the function is increasing
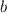 is the decimal form of percentage change.
is the decimal form of percentage change.
Therefore, for b > 1, percentage increase = b - 1
for b < 1, percentage decrease = 1 - b
So as b = 1.09 > 1, percentage increase = 1.09 - 1 = 0.09 = 9%
Part B
From inspection, the amount in account B is increasing exponentially.
Therefore, we can use
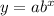
To determine the growth factor
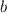 , divide one value of g(r) by its previous value:
, divide one value of g(r) by its previous value:
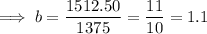
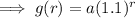
To determine
 , input a pair of values (r, g(r)) into the equation and solve:
, input a pair of values (r, g(r)) into the equation and solve:
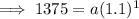
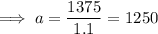
Therefore, the equation for account B:
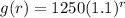
Comparing the growth factor
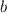 of both equations, account B recorded a greater percentage change in amount of money over the previous year since 1.1 > 1.09
of both equations, account B recorded a greater percentage change in amount of money over the previous year since 1.1 > 1.09