Question

To continually increase the speed of computers, electrical engineers are working on ever-decreasing scales.The size of devices currently undergoing development is measured in nanometers (nm). Engineers fabricating a new transmission-type electron multipliercreated an array of silicon nanopillars on a flat silicon membrane. Subsequently, they measured the diameters (nm) of 50 pillars.

62 74 92 86 92
106 118 68 75 101
93 98 69 80 87
101 77 96 90 97

Group these measurements into a frequency distribution and construct a histogram using (60,701, (70, 801, (80,901, (90,100), (100, 110), (110,120), where the right-hand endpoint is included but the left-hand endpoint is not.

Answer 1

See explanation

Explanation:

The question says the diameters of 50 pillars were measured. However, only the measurements of 20 pillars were provided.

So, I will work with 20

Given

`n = 20`

`62\ 74\ 92\ 86\ 92`

`106\ 118\ 68\ 75\ 101`

`93\ 98\ 69\ 80\ 87`

`101\ 77\ 96\ 90\ 97`

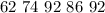
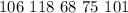
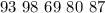
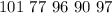
Solving (a): Frequency distribution table

Using the given intervals:

`(60,70]\ => 61 - 70`

`(70, 80] =>71 - 80`

`(80,901]\ =>81 - 90`

`(90,100] =>91 - 100`

`(100, 110] =>101 - 110`

`(110,120] => 111 - 120`

The table is as follows:

`\begin{array}{ccc}{Interval} & {Class\ Mark (x)} & {Frequency (f)} & {61-70} & {65.5} & {3} \ \\ {71-80} & {75.5} & {3} & {81-90} & {85.5} & {3} & {91-100} & {95.5} & {7} & {101-110} & {105.5} & {3} & {111-120} & {115.5} & {1} \ \end{array}`

`Total \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 20`

The class mark is the average of the class interval

For instance: The class mark of 61 - 70 is:

`x = (1)/(2)(61 + 70) = (1)/(2) * 131 = 65.5`

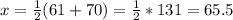
This is applied to other intervals

Solving (b): The histogram

See attachment for histogram

The frequency is plotted on the y-axis while the class interval, on the x-axis.