Solution :
Given :

n = 15
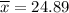
s = 0.5902
The hypothesis :
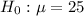

This is a 2 tailed test.
The significance level is
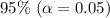
The test statistic :
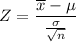
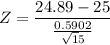
= -0.72
The p value : The p value for Z = -0.72 is 0.4716
The critical value : the critical value at α = 0.05 is +1.96 to -1.96
The decision rule :
If
 or if
or if
 , then reject
, then reject
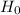 .
.
Also if p value is less than α, then reject
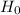 .
.
The decision :
Since the Z falls in between +1.96 and -1.96, we fail to reject the
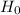 . Also since p value is greater than α, we fail to reject
. Also since p value is greater than α, we fail to reject
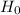 .
.
The conclusion :
There is not sufficient evidence at the 95% significance level to warrant rejection of the claim that the pills come from a population in which the amount of the atorvastatin is equal to 25 mg.
Now calculating the mean and the standard deviation :

Standard deviation =
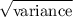
Variance =
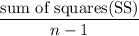
Where, SS =
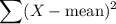
X Mean
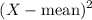
24.1 24.89 0.62
24.4 24.89 0.24
24.3 24.89 0.35
24.9 24.89 0
24.1 24.89 0.62
24.2 24.89 1.72
24.1 24.89 0.04
26.2 24.89 0.04
25.1 24.89 0.24
25 24.89 0.01
24.7 24.89 0.04
25.1 24.89 0.04
25.3 24.89 0.17
25.5 24.89 0.37
25.5 24.89 0.37
n 15
Sum 373.3
Average 24.89
SS 4.8775
Variance =
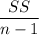 0.348392857
0.348392857
Standard deviation 0.5902