Answer:
The power cost savings for the 8 inches pipe offsets the increased cost for the pipe therefore to save costs the 8-inch pipe should be used
Step-by-step explanation:
The given parameters in the question are;
The distance of the river from the the site, d = 2,500 ft.
The planned flow rate = 600 gal/min
The diameter of the pipe, d = 6-in.
The pipe material = Steel
The cost of pumping = 3 cents per kilowatt-hour
The Bernoulli's equation is presented as follows;



Vₐ - 0 m/s (The river is taken as an infinite source)
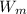 = 0
= 0
The head loss in 6 inches steel pipe of at flow rate of 600 gal/min = 1.19 psi/100 ft
Therefore;
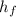 = 1.19 × 2500/100 = 29.75 psi
= 1.19 × 2500/100 = 29.75 psi
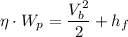
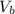 = Q/
= Q/
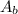 = 600 gal/min/(π·(6 in.)²/4) = 6.80829479 ft./s
= 600 gal/min/(π·(6 in.)²/4) = 6.80829479 ft./s
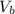 ≈ 6.81 ft./s
≈ 6.81 ft./s
The pressure of the pump = P = 62.4 lb/ft³× (6.81 ft./s)²/2 + 29.75 psi ≈ 30.06 psi
The power of the pump = Q·P ≈ 30.06 psi × 600 gal/min = 7,845.50835 W
The power consumed per hour = 7,845.50835 × 60 × 60 W
The cost = 28,243.8301 kW × 3 = $847.31 per hour
Annual cost = $847.31 × 8766 = $7,427,519.46
Pipe cost = $15/ft × 2,500 ft = $37,500
Annual charges = 20% × Installed cost = 0.2 × $37,500 = $7,500
Total cost = $37,500 + $7,500 + $7,427,519.46 = $7,475,519.46
For the 8-in pipe, we have;
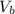 = Q/
= Q/
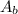 = 600 gal/min/(π·(8 in.)²/4) = 3.83 ft./s
= 600 gal/min/(π·(8 in.)²/4) = 3.83 ft./s
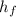 = 1.17 ft/100 feet
= 1.17 ft/100 feet
Total head loss = (2,500 ft/100 ft) × 1.17 ft. = 29.25 ft.

∴
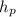 = (3.83 ft./s)²/(2 × 32.1740 ft/s²) + 29.25 ft. ≈ 29.5 ft.
= (3.83 ft./s)²/(2 × 32.1740 ft/s²) + 29.25 ft. ≈ 29.5 ft.
The power of the pump = ρ·g·h × Q
Power of pump = 62.4 lb/ft³ × 32.1740 ft/s² × 29.5 ft.× 600 gal/min = 3,363.8047 W
The cost power consumed per annum = 3,363.8047 W × 60 × 60 × 3 × 8766 = $3,184,608.1
The Cost of the pipe = $20/ft × 2,500 ft. = $50,000
The total cost plus charges = $3,184,608.1 + $50,000 + $10,000 = $3,244,608.1
Therefore it is more affordable to use the 8-in pipe which provides substantial savings in power costs