The quadratic function represented by the given graph is
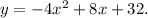
The quadratic function represented by the given graph can be determined by finding its equation in the form of
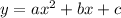 , where a, b, and c are constants.
, where a, b, and c are constants.
To find the equation, we can use the points (-2, 0), (2, 32), and (4, 0) that are on the graph.
Step 1: Substitute the coordinates of the points into the equation
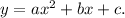
Using the point (-2, 0):
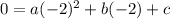
Using the point (2, 32):
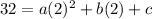
Using the point (4, 0):
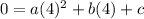
Step 2: Solve the resulting system of equations to find the values of a, b, and c.
From the equation
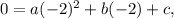 we get:
we get:
4a - 2b + c = 0 ------ (1)
From the equation
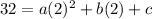 , we get:
, we get:
4a + 2b + c = 32 ------ (2)
From the equation
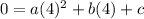 , we get:
, we get:
16a + 4b + c = 0 ------ (3)
Step 3: Solve the system of equations (1), (2), and (3).
Subtracting equation (1) from equation (2), we get:
4a + 2b + c - (4a - 2b + c) = 32 - 0
4b = 32
b = 8
Substituting b = 8 into equation (1), we get:
4a - 2(8) + c = 0
4a - 16 + c = 0
4a + c = 16
c = 16 - 4a
Substituting b = 8 and c = 16 - 4a into equation (3), we get:
16a + 4(8) + (16 - 4a) = 0
16a + 32 + 16 - 4a = 0
12a + 48 = 0
12a = -48
a = -4
Step 4: Substitute the values of a, b, and c back into the equation y = ax^2 + bx + c.
Therefore, the quadratic function represented by the graph is:
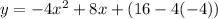
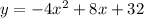 .
.