Question

A physical education teacher wanted to know the effects of various activity levels on body composition. She surveyed her physical education classes and categorized 30 students into five activity levels based on the amount of daily exercise in which the students participated: inactive, semiactive, normal, active, and very active. She measured percent body fat values using skinfold calipers on all subjects with the following results.

Inactive Semiactive Normal Active Very Active
30.2 29.4 22.9 17.6 10.9
29.6 17.6 25.4 13.4 13.7
35.2 26.4 19.6 20.3 12.8
19.1 25.3 18.7 19.6 14.7
26.3 22.5 21.8 15.1 9.3
22.4 28.6 24.9 10.7 12.7

Required:
a. What is the independent variable in this study? What is the dependent variable?
b. What are the means and standard deviations for each group?
c. Does a significant difference exist among any of the groups?

Answer 1

a. The independent variable is the activity level

The dependent variable is the body composition (the percentage of body fat in the values)

b. The mean and standard deviation are;

(Mean, Standard deviation)

Inactive(27.13, 5.8), Semiactive(24.97, 4.367), Normal(22.217, 2.73), Active(16.12, 3.73), Very Active (12.35, 1.95)

c. Yes

Between Semiactive and Active, Semiactive and Very Active, Normal and Very Active, Normal and Active, Active and Inactive, and Inactive and Very Active

Explanation:

a. The independent variable is the activity level

The dependent variable is the body composition (the percentage of body fat in the values)

b. The given data are presented as follows;

Inactive
`{}` Semiactive Normal Active Very Active

30.2
`{}` 29.4 22.9 17.6 10.9

29.6
`{}` 17.6 25.4 13.4 13.7

35.2
`{}` 26.4 19.6 20.3 12.8

19.1
`{}` 25.3 18.7 19.6 14.7

26.3
`{}` 22.5 21.8 15.1 9.3

22.4
`{}` 28.6 24.9 10.7 12.7

Bymaking use of Microsoft Excel, we have;

Inactive
`{}` Semiactive Normal Active Very Active

Mean 27.13
`{}` 24.97 22.217 16.12 12.35

Standard Deviation 5.8
`{}`
`{}` 4.367 2.73 3.73 1.95

c. Yes

`t=\frac{(\bar{x}_(1)-\bar{x}_(2)) }{\sqrt{(s_(1)^(2) )/(n_(1))-(s _(2)^(2))/(n_(2))}}`

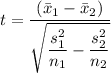
The degrees of freedom = n - 1 = 6 - 1 = 5

The critical t = 2.5706

Therefore, we have;

The test statistic for Inactive and semi active ≈ 0.72875

The test statistic for Semiactive Normal ≈ 1.309

The test statistic for Inactive and Normal ≈ 1.8773

The test statistic for Semiactive and Active ≈ 3.775 (Significant)

The test statistic for Semiactive and Very Active ≈ 6.464 (Significant)

The test statistic for Normal and Very Active ≈ 7.204 (Significant)

The test statistic for Normal and Active ≈ 3.231 (Significant)

The test statistic for Active and Inactive ≈ 3.91 (Significant)

The test statistic for Active and Very Active ≈ 2.194

The test statistic for Inactive and Very Active ≈ 5.92 (Significant)

Where the test statistic is larger than the critical 't' the statistic is significant