Answer:
B. 134,700
Explanation:
m =
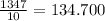
g = 0
Step by Step Solution
More Icon
Reformatting the input :
Changes made to your input should not affect the solution:
(1): "134.7" was replaced by "(1347/10)".
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
(1347/10)*g-(m*g)=0
Step by step solution :
STEP
1
:
1347
Simplify ————
10
Equation at the end of step
1
:
1347
(———— • g) - gm = 0
10
STEP
2
:
Rewriting the whole as an Equivalent Fraction
2.1 Subtracting a whole from a fraction
Rewrite the whole as a fraction using 10 as the denominator :
gm gm • 10
gm = —— = ———————
1 10
Equivalent fraction : The fraction thus generated looks different but has the same value as the whole
Common denominator : The equivalent fraction and the other fraction involved in the calculation share the same denominator
Adding fractions that have a common denominator :
2.2 Adding up the two equivalent fractions
Add the two equivalent fractions which now have a common denominator
Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible:
1347g - (gm • 10) 1347g - 10gm
————————————————— = ————————————
10 10
STEP
3
:
Pulling out like terms :
3.1 Pull out like factors :
1347g - 10gm = -g • (10m - 1347)
Equation at the end of step
3
:
-g • (10m - 1347)
————————————————— = 0
10
STEP
4
:
When a fraction equals zero :
4.1 When a fraction equals zero ...
Where a fraction equals zero, its numerator, the part which is above the fraction line, must equal zero.
Now,to get rid of the denominator, Tiger multiplys both sides of the equation by the denominator.
Here's how:
-g•(10m-1347)
————————————— • 10 = 0 • 10
10
Now, on the left hand side, the 10 cancels out the denominator, while, on the right hand side, zero times anything is still zero.
The equation now takes the shape :
-g • (10m-1347) = 0
Theory - Roots of a product :
4.2 A product of several terms equals zero.
When a product of two or more terms equals zero, then at least one of the terms must be zero.
We shall now solve each term = 0 separately
In other words, we are going to solve as many equations as there are terms in the product
Any solution of term = 0 solves product = 0 as well.
Solving a Single Variable Equation:
4.3 Solve : -g = 0
Multiply both sides of the equation by (-1) : g = 0
Solving a Single Variable Equation:
4.4 Solve : 10m-1347 = 0
Add 1347 to both sides of the equation :
10m = 1347
Divide both sides of the equation by 10:
m = 1347/10 = 134.700
Two solutions were found :
m = 1347/10 = 134.700
g = 0