Answer:
Vertex:
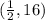
Zeros:
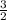 and
and
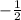
Explanation:
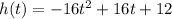
1) Find the x-coordinate of the vertex
 where the equation is
where the equation is

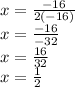
2) Find the y-coordinate of the vertex
Plug the x-coordinate
 back into the original equation
back into the original equation
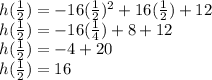
Therefore, the vertex of the parabola is
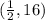 .
.
3) Find the zeros of the parabola
Rewrite the equation so that it equals 0
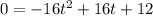
Divide both sides by -16

Simplify the fraction
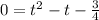
Complete the square; first isolate t²-t
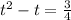
Complete the square; Add
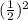 to both sides
to both sides
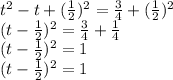
Take the square root of both sides

Isolate t
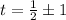
Find the zeros
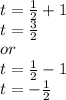
Therefore, the zeros of the parabola are
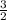 and
and
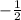 .
.
I hope this helps!