Question

PLEASE ANSWER THIS IF YOU KNOW IT!! AND HURRY!!​

Answer 1

The shorter leg, s, is the geometric mean between h and m

The longer leg, b, is the geometric mean between h and n

Explanation:

By the right triangle geometric mean theorem, we have;

The altitude of a right triangle, 'h', which intersects with the hypotenuse side of the right triangle at a point such that it creates two segments, 'a' and 'b' on the hypotenuse side , then we have;

h = √(a·b)

Therefore, we have;

Description
`{}` Proportion

The altitude of ΔAYES is the geometric mean between m and n
`(m)/(a) =(a)/(n)`

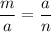
a² = m·n → a = √(m·n)

The shorter leg, s, is the geometric mean between h and m
`(m)/(s) =(s)/(h)`

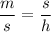
s² = m·h → s = √(m·h)

The longer leg, b, is the geometric mean between h and n
`(n)/(b) =(b)/(h)`

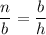
b² = n·h → s = √(n·h)