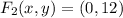Answer:
The standard form of the ellipse is
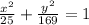 . Coordinates of the foci are
. Coordinates of the foci are
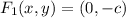 and
and
 , respectively.
, respectively.
Explanation:
The equation of a ellipse centered in the origin in standard form is defined by following formula:
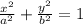 (1)
(1)
Where
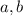 are the coefficients of the ellipse.
are the coefficients of the ellipse.
Now we proceed to transform the equation of the ellipse in general form into standard form by algebraic means:

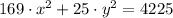
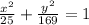
Since
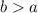 , then major axis of the ellipse is located in y-axis. The distance between center and focus (
, then major axis of the ellipse is located in y-axis. The distance between center and focus (
 ) is calculated by following Pythagorean identity:
) is calculated by following Pythagorean identity:
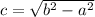 (2)
(2)

The location of the foci are represented by
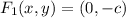 and
and
 . If we know that
. If we know that
 , then the location of the foci are, respectively:
, then the location of the foci are, respectively:
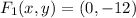 ,
,