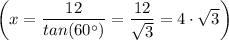Question

(Picture for problem above.)

Find the value of y. Be sure to keep the exact value (use square root and don’t round your answer).

Answer 1

y = 8·√3

Explanation:

From the drawing of the right triangle, we have;

The length of the opposite leg to the given 60° (reference) angle = 12

The length of the adjacent leg to given 60° (reference) angle = x

The length of the hypotenuse side = y

By trigonometric ratios, we have;

`sin(Reference \, Angle) = (Opposite \ leg \ length)/(Hypotenuse \ length)`

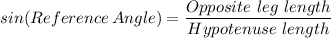
Therefore, we have;

`sin(60^\circ) = (12)/(y)`

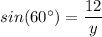
From the value of sin(60°), we have;

`sin(60^\circ) = (√(3) )/(2)`

`\therefore y= (12)/(sin(60^\circ) ) = (12)/((√(3) )/(2) ) = \frac{2 * 12 * √(3) }{{{3} } } = \frac{24 * √(3) }{{{3} } } = 8 \cdot √(3)`

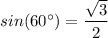
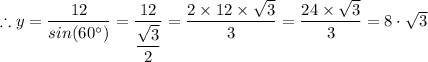
y = 8·√3

`\left(x= (12)/(tan(60^\circ) ) = \frac{12}{{√(3) } } = 4\cdot √(3) \right)`