Hi there!
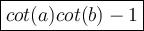
We can begin by simplifying cos(a + b) to find an equivalent expression.
With a sum of angles identity for cosine, we can determine that:
cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
In this instance, we have to multiply this expression by csc(a)csc(b). Therefore:
(csc(a)csc(b)) · (cos(a)(cos(b) - sin(a)sin(b))
Distribute:
(csc(a)(csc(b))(cos(a)(cos(b)) - (csc(a)csc(b))(sin(a)sin(b))
Rewrite csc as 1/sin to simplify:
(1/sin(a) * 1/sin(b))(cos(a)(cos(b)) - (1/sin(a) * 1/sin(b))(sin(a)sin(b))
Multiply:
cos(a)/sin(a) * cos(b)/sin(b) - 1/sin(a) * sin(a) * 1/sin(b)*sin(b) <--- = 1
We now have remaining:
cos(a) / sin(a) * cos(b)/sin(b) - 1
Simplify to cotangent:
cot(a) * cot(b) - 1