Question

(1/27)^x-6=27

Could I please have a step by step as well? Much appreciated! ​

Answer 1

`x = 7`

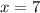
Explanation:

1) Use Division Distributive Property: (x/y)^a = x^a/y^a.

`\frac{1}{ {27}^(x - 8) } = 27`

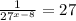
2) Multiply both sides by 27^x - 8.

`1 = {27} * 27^(1 + x - 8)`

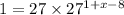
3) Use the product rule: x^a x^b = x^a+b.

`1 = {27}^(1 + x - 8)`

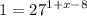
4) Simplify 1 + x - 8 to x - 7.

`1 = {27}^(x - 7)`

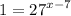
5) Use Definition of Common Logarithm: b^a = x if and only if logb (x) = a.

`log_(27)1 = x - 7`

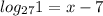
6) Use Change of Base Rule.

`\frac{ log_1 }{ log{27} } = x - 7`

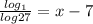
7) Use rule of 1: log 1 = 0.

`(0)/( log_(27)) = x - 7`

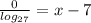
8) Simplify 0/log_27 to 0.

`0 = x - 7`

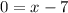
9) Add 7 to both sides.

`7 = x`

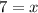
10) Switch sides.

`x = 7`

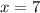
Therefor, the answer is x = 7.