Problem 1, part (a)

Answer: 107 degrees
======================================================
Problem 1, part (b)
The previous result (107) is neither 0, nor 90, nor 180. This means the vectors are neither parallel nor perpendicular.
Answer: Neither
======================================================
Problem 2, part (a)
We follow the same idea as problem 1, part (a). Just with different numbers of course.
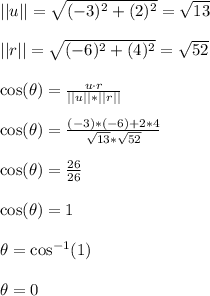
Answer: 0
======================================================
Problem 2, part (b)
The lines are parallel because of the angle of 0 degrees between the vectors. The angles point in the same direction.
Answer: Parallel