I saw on your other question that you mention y (0) = 0. Let
f(x, y) = x + y ²
Now consider the recurrences in Euler's method,
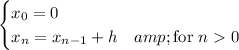
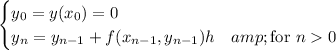
where h is the step size.
We then approximate y (0.2) in ...
• ... 2 steps for h = 0.1 :
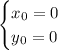
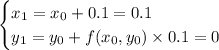
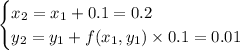
so that y (0.2) ≈ 0.01;
• ... 4 steps for h = 0.05 :
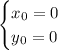
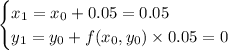
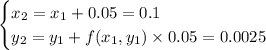
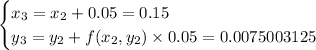
![\begin{cases}x_4=x_3+0.05=0.2\\y_4=y_3+f(x_3,y_3)*0.05=0.0150031252343798828125]()
so y (0.2) ≈ 0.015.