Answer:
Part 1)
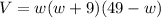
Part 2)
We can have the aquarium have a width of 40 inches, a height of 49 inches, and a length of 9 inches.
Or we can have the aquarium have a width of 21 inches, a height of 30 inches, and a length of 28 inches.
Explanation:
The dimensions of the aquarium is as follows:
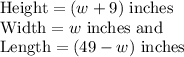
Part 1)
We want to find a polynomial expression that represents the volume of the aquarium according to the specified dimensions.
Since the aquarium is a rectangular prism, the volume will simply be the product of all the dimensions. Hence:
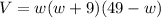
Part 2)
We want to aquarium to hold 17, 640 cubic inches of water. In other words, the volume V should be 17640. Thus:
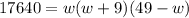
First, we can distribute the right-hand side:
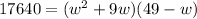
Distribute:

Distribute:
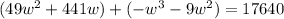
Simplify:
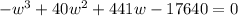
Now, we can factor. From the first two terms, factor out a -w² and from the second two terms, we can factor out 441:
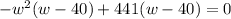
Grouping:
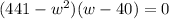
Zero Product Property:

Solve for each case:
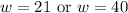
So, we have two possible sets of dimensions.
We can have the aquarium have a width of 40 inches, a height of 49 inches, and a length of 9 inches.
Or we can have the aquarium have a width of 21 inches, a height of 30 inches, and a length of 28 inches.