Question

Y’ =2x - 3y + 1,y(1) = 5; y(1.2)

Answer 1

Applying Euler's method:

Let f(x, y) = 2x - 3y + 1, and consider the following recurrence relations:

`\begin{cases}x_0=1\\x_n=x_(n-1)+h&\text{for }n\ge1\end{cases}`

`\begin{cases}y_0=5\\y_n=y_(n-1)+f(x_n,y_n)h&\text{for }n\ge1\end{cases}`

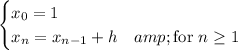
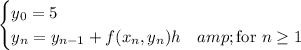
For step size h = 0.1, we can approximate y (1.2) with just 2 steps:

`\begin{cases}x_0=1\\y_0=5\end{cases}\implies y_1=5+f(1,5)*0.1=3.8`

`\begin{cases}x_1=1+0.1=1.1\\y_1=3.8\end{cases}\implies y_2=3.8+f(1.1,3.8)*0.1=\boxed{2.98}`

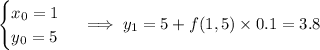
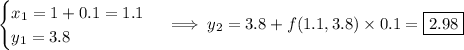
For step size h = 0.05, we need 4 steps:

`\begin{cases}x_0=1\\y_0=5\end{cases}\implies y_1=5+f(1,5)*0.05=4.4`

`\begin{cases}x_1=1+0.05=1.05\\y_1=4.4\end{cases}\implies y_2=4.4+f(1.05,4.4)*0.05=3.895`

`\begin{cases}x_2=1.05+0.05=1.1\\y_2=3.895\end{cases}\implies y_3=3.895+f(1.1,3.895)*0.05=3.47075`

`\begin{cases}x_3=1.1+0.05=1.15\\y_3=3.47075\end{cases}\implies y_4=3.47075+f(1.15,3.47075)*0.05\approx\boxed{3.1151375}`

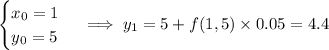
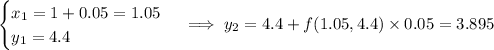
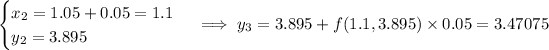
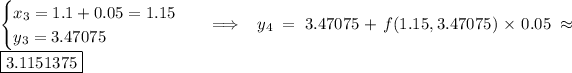
(Compare these to the value of y (1.2) found using the exact solution to the differential equation, about 3.22832.)