Answer:
Determine the slopes (gradients) of each line.
If the slopes of two of the lines are negative reciprocals (if their product is -1), the lines are perpendicular (the vertex is 90°).
Using slope formula:
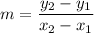
Slope of AC:
A = (1, 1) =
C = (7, 7) =
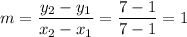
Slope of AB:
A = (1, 1) =
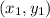
B = (10, 4) =
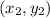
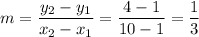
Slope of BC:
B = (10, 4) =
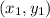
C = (7, 7) =
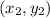
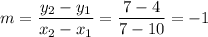
Therefore, as AC and BC are negative reciprocals of each other (1 x -1 = -1), m∠C = 90° which proves that the triangle is a right triangle.