Question

Given the two functions, which statement is true?

(function is in picture)

A) g(x) is stretched vertically by a factor of 2 and shifted to the right 4 units compared to f(x).


B) g(x) is shrunk vertically by a factor of ½ and shifted to the right 4 units compared to f(x).


C) g(x) is stretched vertically by a factor of 2 and shifted to the left 4 units compared to f(x).


D) g(x) is shrunk vertically by a factor of ½ and shifted to the left 4 units compared to f(x).

Answer 1

Option D

Explanation:

f(x) =
`\text{log}_(15)x`

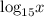
Transformed form of the function 'f' is 'g'.

g(x) =
`(1)/(2)\text{log}_(15)(x+4)`

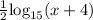
Property of vertical stretch or compression of a function,

k(x) = x

Transformed function → m(x) = kx

Here, k = scale factor

1). If k > 1, function is vertically stretched.

2). If 0 < k < 1, function is vertically compressed.

From the given functions, k =
`(1)/(2)`

Since, k is between 0 and
`(1)/(2)`, function f(x) is vertically compressed by a scale factor
`(1)/(2)`.

g(x) = f(x + 4) represents a shift of function 'f' by 4 units left.

g(x) = f(x - 4) represents a shift of function 'f' by 4 units right.

g(x) =
`(1)/(2)\text{log}_(15)(x+4)`

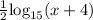
Therefore, function f(x) has been shifted by 4 units left to form image function g(x).

Option D is the answer.