Answers are in bold.
22. b/c
24. sqrt(17)/17
26. 1/4
28. sqrt(17)/17
30. 1/2
32. sqrt(2)/2
34. sqrt(3)/2
36. Approximately 5.4077 units
=====================================================
Step-by-step explanation:
Problem 22
To get the cosine ratio, we divide the adjacent over hypotenuse.
cos(angle) = adjacent/hypotenuse
cos(x) = b/c
----------------------------------
Problem 24
To get the sine ratio, we divide opposite over hypotenuse.
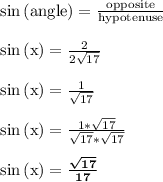
In the fourth step, I multiplied top and bottom by sqrt(17) to rationalize the denominator.
----------------------------------
Problem 26
tan(angle) = opposite/adjacent
tan(x) = 2/8
tan(x) = 1/4
----------------------------------
Problem 28
cos(y) = sin(x) in this case. The general rule is that sin(A) = cos(B) if and only if A+B = 90.
Therefore the answer is exactly identical to problem 24.
----------------------------------
Problem 30
sin(30) = 1/2 is something you either memorize or look up on a reference chart, or use the unit circle. Alternatively, you can use a 30-60-90 triangle template.
----------------------------------
Problem 32
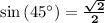 is something you memorize or have on a reference sheet. You could also use a 45-45-90 triangle.
is something you memorize or have on a reference sheet. You could also use a 45-45-90 triangle.
----------------------------------
Problem 34
 is similar to problems 30 and 32 in that you should memorize this or have it on a reference sheet. You could use a 30-60-90 triangle template here.
is similar to problems 30 and 32 in that you should memorize this or have it on a reference sheet. You could use a 30-60-90 triangle template here.
----------------------------------
Problem 36
Let x be the length of side AC.
Use the tangent ratio to find x.
tan(angle) = opposite/adjacent
tan(B) = AC/AB
tan(31) = x/9
x = 9*tan(31)
x = 5.4077 approximately