Answer:
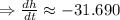
Step-by-step explanation:
The volume of a cone, V = 1/3πr^2h
Where r is the radius, and h is the height of the cone.
Given:
Volume is constant at 56 cubic feet.
Radius of cone increases at a constant rate of 8 feet per second.
The radius of the cone is 3 feet.
When radius is 3 feet
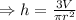

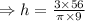
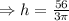
Where h is in feets.
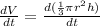


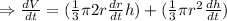
Since the volume is constant so
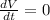
The rate of change of radius is
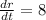

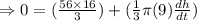
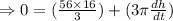
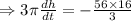
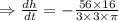
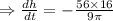
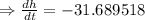
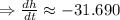
The minus indicates that the rate of change of height is decreasing.