3 Answers:
========================================================
Step-by-step explanation:
Multiply the given radian angle measure by the fraction 180/pi to convert to degree form.
This gives
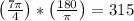
The pi terms cancel.
Therefore, 7pi/4 radians = 315 degrees.
----------------------------
Use the unit circle (see below) to see that 315 degrees is in quadrant 4.
The terminal point that corresponds to this angle is
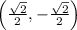
This leads us to
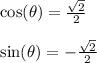
Since any point on the unit circle is of the form
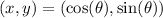
The ratio of those sine and cosine values leads to the tangent value.
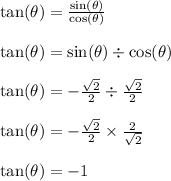
----------------------------------
Go back to the 315 degree angle.
This angle is between 270 and 360, so it's in Q4.
The reference angle for anything in Q4 is 360-theta
So the reference angle here is 360-theta = 360-315 = 45.