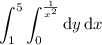(1) The integral is straightforward; x ranges between two constants, and y ranges between two functions of x that don't intersect.

(2) First find where the two curves intersect:
y ² - 4 = -3y
y ² + 3y - 4 = 0
(y + 4) (y - 1) = 0
y = -4, y = 1 → x = 12, x = -3
That is, they intersect at the points (-3, 1) and (12, -4). Since x ranges between two explicit functions of y, you can capture the area with one integral if you integrate with respect to x first:
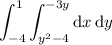
(3) No special tricks here, x is again bounded between two constants and y between two explicit functions of x.