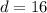Answer:
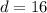
General Formulas and Concepts:
Pre-Algebra:
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
Algebra II
- Distance Formula:
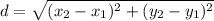
Explanation:
Step 1: Define
Point M(-21, -7)
Point N(-5, -7)
Step 2: Identify
M(-21, -7) → x₁ = -21, y₁ = -7
N(-5, -7) → x₂ = -5, y₂ = -7
Step 3: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d
- Substitute in points [Distance Formula]:
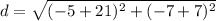
- [Distance] [√Radical] (Parenthesis) Add:
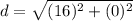
- [Distance] [√Radical] Evaluate exponent:
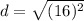
- [Distance] Evaluate radical: