Question

A golfer hits an errant tee shot that lands in the rough. A marker in the center of the fairway is 150 yards from the center of the green. While

standing on the marker and facing the green, the golfer turns 100° towards his ball. He then paces off 30 yards to his ball. How far is the
ball from the center of the green?
150 yd

Answer 1

`\bold{\huge{\underline{ Solution}}}`

Given :-

• A marker in the center of the fairway is 150 yards away from the centre of the green
• While standing on the marker and facing the green, the golfer turns 100° towards his ball
• Then he peces off 30 yards to his ball

To Find :-

• We have to find the distance between the golf ball and the center of the green .

Let's Begin :-

Let assume that the distance between the golf ball and central of green is x

Here,

• Distance between marker and centre of green is 150 yards
• That is, Height = 150 yards
• For facing the green , The golfer turns 100° towards his ball
• That is, Angle = 100°
• The golfer peces off 30 yards to his ball
• That is, Base = 30 yards

According to the law of cosine :-

`\bold{\red{ a^(2) = b^(2) + c^(2) - 2ABcos}}{\bold{\red{\theta}}}`

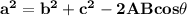
• Here, a = perpendicular height
• b = base
• c = hypotenuse
• cos theta = Angle of cosine

So, For Hypotenuse law of cosine will be :-

`\sf{ c^(2) = a^(2) + b^(2) - 2ABcos}{\sf{\theta}}`

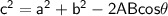
Subsitute the required values,

`\sf{ x^(2) = (150)^(2) + (30)^(2) - 2(150)(30)cos}{\sf{100°}}`

`\sf{ x^(2) = 22500 + 900 - 900cos}{\sf{*{(5π)/(9)}}}`

`\sf{ x^(2) = 22500 + 900 - 900( - 0.174)}`

`\sf{ x^(2) = 22500 + 900 + 156.6}`

`\sf{ x^(2) = 23556.6}`

`\bold{ x = 153.48\: yards }`

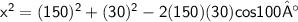
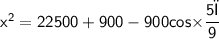
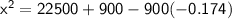
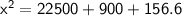
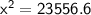
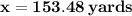
Hence, The distance between the ball and the center of green is 153.48 or 153.5 yards