Question

Given triangle abc with vertices A(2,-1), B(5,6), C(-1,4) as shown. Find the number of square units in the area of triangle abs in simplest form.

Answer 1

The area of the triangle is 18 square units.

Explanation:

First, we determine the lengths of segments AB, BC and AC by Pythagorean Theorem:

AB

`AB = \sqrt{(5-2)^(2)+[6-(-1)]^(2)}`

`AB \approx 7.616`

BC

`BC = \sqrt{(-1-5)^(2)+(4-6)^(2)}`

`BC \approx 6.325`

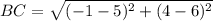
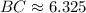
AC

`AC = \sqrt{(-1-2)^(2)+[4-(-1)]^(2)}`

`AC \approx 5.831`

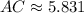
Now we determine the area of the triangle by Heron's formula:

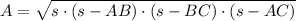`A = √(s\cdot (s-AB)\cdot (s-BC)\cdot (s-AC))` (1)

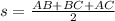`s = (AB+BC + AC)/(2)` (2)

Where:

`A` - Area of the triangle.

`s` - Semiparameter.

If we know that
`AB \approx 7.616`,
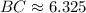`BC \approx 6.325` and
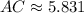`AC \approx 5.831`, then the area of the triangle is:

`s \approx 9.886`

`A = 18`

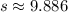
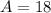
The area of the triangle is 18 square units.