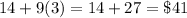Answer:
The two siblings will have saved the same amount towards their mother's gift after 3 weeks.
Amount saved by Wyatt =
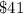
Amount saved by Wyatt's sister =
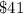
Explanation:
Let
 (in weeks) denotes the time period by which the two siblings will have saved the same amount towards their mother's gift.
(in weeks) denotes the time period by which the two siblings will have saved the same amount towards their mother's gift.
Wyatt already has $20 saved and plans to save $7 per week from his allowance.
Amount saved by Wyatt =
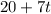
Wyatt's sister has $14 saved so far and will save $9 per week from hers.
Amount saved by Wyatt's sister =
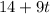
To find the time period by which the two siblings will have saved the same amount towards their mother's gift,
solve the following equation.

So, the two siblings will have saved the same amount towards their mother's gift after 3 weeks.
Amount saved by Wyatt =
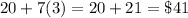
Amount saved by Wyatt's sister =