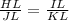Question:
 HLI is shown. Line segment JK is drawn near point L to create
HLI is shown. Line segment JK is drawn near point L to create
 JLK. If
JLK. If
 HLI ~
HLI ~
 JLK by the SSS similarity theorem, then
JLK by the SSS similarity theorem, then
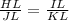 is also equal to which ratio?
is also equal to which ratio?
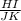

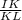
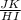
Answer:
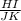
Explanation:
Given
HLI ~
 JLK
JLK
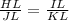
Required
Which other ratio equals
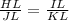
 HLI ~
HLI ~
 JLK implies that:
JLK implies that:
HL, IL and HI corresponds to JL, KL and JK respectively.
So, the possible ratios are:
HL : IL : HI = JL : KL : JK
Convert to fractions

So, from the list of options
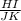 is equivalent to
is equivalent to