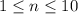Answer:
 --- Job offer 1
--- Job offer 1
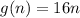 --- Job offer 2
--- Job offer 2
Explanation:
Given
Job offer 1:
Offer = $0.25
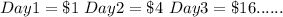
Job offer 2:
Daily = $16
Required
Determine the equation for both jobs
For job offer 1:
Considering the pay for day 1, day 2,....
The sequence shows a geometry progression where the payment between subsequent days is a product of 4 by the payment of the previous day.
The sequence can be represented as:
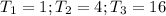
The common ratio (r) is:
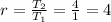
The sum of n terms is the total salary received in n days.

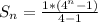
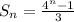
So, the equation for job offer 1 is:


Take LCM
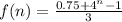
Collect like terms
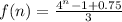

For job offer 2:
Daily payment of $16 implies that job offer 2 pays 16n for n days.
So:
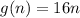
In both cases: