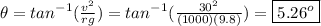Question

A car moves along a curved road of diameter 2 km. If the maximum velocity for safe driving on this path is 30 m/s, at what angle has the road been banked? (Ignore friction.)

A) 11°
B) 22.6°
C) 45.2°
D) 5.26°

Answer 1

Hi there!

Ignoring friction, we know that the centripetal force experienced by the car is due to the normal force exerted by the road.

We can do a summation of forces in both the horizontal and vertical directions.

Vertical:

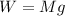`W = Mg`, force due to gravity

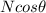`Ncos\theta`, VERTICAL component of the normal force.

`\Sigma F_y = Ncos\theta - Mg\\\\Mg = Ncos\theta`

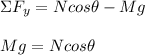
Horizontal:

`Nsin\theta = F_(Hnet)`

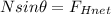
The net horizontal force is equivalent to the centripetal force:

`Nsin\theta = (mv^2)/(r)`

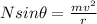
We can solve for theta by dividing:

`(Nsin\theta = (mv^2)/(r))/(Ncos\theta = mg)`

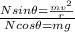
Simplify:

`tan\theta = ( (v^2)/(r))/( g)\\\\tan\theta =(v^2)/(rg)`

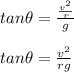
Solve:

`\theta = tan^(-1)((v^2)/(rg)) = tan^(-1)((30^2)/((1000)(9.8))) = \boxed{5.26^o}`