Given:
The vertices of a right triangle are:
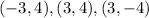
To find:
The length of the hypotenuse of the given right triangle.
Solution:
Let the vertices of the right triangle are
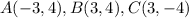 .
.
The distance formula is:
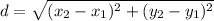
Using distance formula, we get
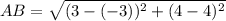
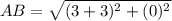
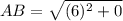
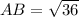
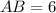
Similarly,
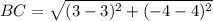
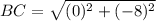
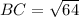
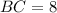
And,
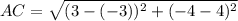
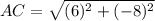
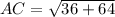
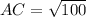
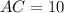
Now, taking sum of squares of two smaller sides, we get
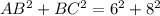
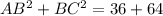
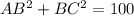
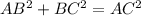
By the definition of the Pythagoras theorem, AC is the hypotenuse of the given triangle.
Therefore, the length of the hypotenuse is 10 units.