Answer: D) 101
Explanation:
By linearity, we can break it up into 2 integrals. The integral and derivative of f easily cancel out
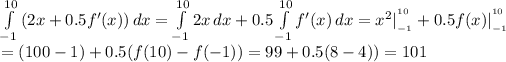
I used the table for values of f(x) at 10 and -1. Wouldn't be surprised if this was part of a series of questions about f because I really can't see how you could use the hypothesis that f is twice differentiable on R. Same for the other table values. I'm curious about how you found the answer. Was it a different way?