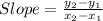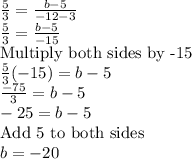Question

A line passes through the origin (3,5) and (-12, b) what is the value of B?

Answer 1

b = -20

Explanation:

Let's start by finding the slope of the line.

`Slope=(y_2-y_1)/(x_2-x_1)`

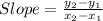
Origin: (0, 0)

We can use (0, 0) and (3, 5) to find the slope:

`Slope=(5-0)/(3-0)=(5)/(3)`

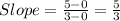
Then, we can plug this into the equation for slope to find the value of b (the slope has to be the same, since they're on the same line)

`Slope=(y_2-y_1)/(x_2-x_1)`

`(5)/(3)=(b-5)/(-12-3)\\(5)/(3)=(b-5)/(-15)\\\text{Multiply both sides by -15}\\(5)/(3)(-15)=b-5\\(-75)/(3)=b-5\\-25=b-5\\\text{Add 5 to both sides}\\b=-20`