Answer:
There are 16 terms in the expansion.
Explanation:
Number of terms in a binomial expansion:
The number of terms in a binomial expansion
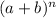
Is n + 1.
Power property:
For a power elevated to another power, we have that:
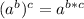
In this question:
![[(3x^2 + 7x)^3]^5 = (3x^2 + 7x)^(3*5) = (3x^2 + 7x)^(15)](https://img.qammunity.org/2022/formulas/mathematics/college/snp9ch98sz9g6h86msp871dgbpr8l1fi8u.png)
So
 , then the number of terms is
, then the number of terms is

There are 16 terms in the expansion.