Question

Please I need someone to help my assignment​

Answer 1

Answer: x = 10

Explanation:

The Pythagorean's theorem says that for a triangle rectangle with catheti A and B, and with hypotenuse H, we have:

A^2 + B^2 = H^2

In this case, we have:

A = (x - 4)

B = (x - 2)

H = x

Then we have the equation:

(x - 4)^2 + (x - 2)^2 = x^2

Now we need to solve this for x, first let's simplify it.

(x^2 - 2*x*4 + 16) + (x^2 - 2*2*x + 4) = x^2

2*x^2 - 12*x + 20 = x^2

2*x^2 - 12*x + 20 - x^2 = 0

x^2 - 12*x + 20 = 0

The solutions of this equation are given by the Bhaskara's equation, such that for an equation like:

a*x^2 + b*x + c = 0

The solutions are:

`x = (-b \pm √(b^2 - 4*a*c) )/(2*a)`

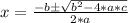
Then the solutions for our equation are:

`x = (-(-12) \pm √((-12)^2 - 4*1*20) )/(2*1) = (12 \pm 8 )/(2)`

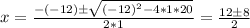
Then the two possible solutions are:

x = (12 - 8)/2 = 4/2 = 2

Notice that if x = 2, then the length of the catheti will be:

A = 2 - 4 = -2

B = 2 - 2 = 0

This has no sense, so we can discard this solution.

The other solution for x is:

x = (12 + 8)/2 = 10

x = 10

Then:

H = 10

A = 10 - 4 = 6

B = 10 - 2 = 8

This solution makes sense, then x = 10.