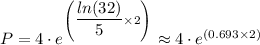Question

While growing bacteria in a laboratory Petri dish, a scientist notices the number of bacteria over time. The observations are shown in the table.

Number of bacteria
Number of minutes
from initial state
0 4
5 128
10 4096
15 131072

What function can be used to describe the number (n) of bacteria after 2 minutes?

Answer 1

The function that can be used to describe the number (n) of bacteria after 2 minutes is;

`P = 4 \cdot e^{\left((ln(32))/(5) * 2\right)} \approx 4 \cdot e^(\left(0.693* 2\right))`

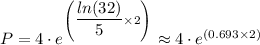
Explanation:

The data in the table are presented as follows;

Number of bacteria; 4, 128, 4,096, 131,072

Number of minutes from initial state; 0, 5, 10, 15

The general equation for population growth is presented as follows;

`P = P_0 \cdot e^(r\cdot t)`

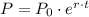
Where;

P = The population after 't' minutes

P₀ = The initial population

r = The population growth rate

t = The time taken for the growth in population numbers

At t = minutes. we have;

`4 = P_0 \cdot e^(r*0) = P_0`

∴ P₀ = 4

At t = 5, we have;

`128 = 4 \cdot e^(r* 5)`

`\therefore e^(r* 5) = (128)/(4) = 32`

`ln\left(e^(r* 5)\right) = ln(32)`

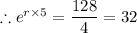
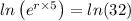
∴ r × 5 = ㏑(32)

r = ln(32)/5 ≈ 0.693

The number (n) of bacteria after 2 minutes is therefore;

`P = 4 \cdot e^{\left((ln(32))/(5) * 2\right)} \approx 4 \cdot e^(\left(0.693* 2\right))`