Question

A student makes a homemade resistor from a graphite pencil 5.00 cm long, where the graphite is 0.05 mm in diameter. The resistivity of the graphite is rho=1.38×10−5Ω/mrho=1.38×10−5Ω/m . The homemade resistor is place in series with a switch, a 10.00-mF uncharged capacitor and a 0.50-V power source. (a) What is the RC time constant of the circuit? (b) What is the potential drop across the pencil 1.00 s after the switch is closed?

Answer 1

(a) RC time constant of the circuit is 6.9 × 10⁻⁶ ms

(b) The potential drop across the capacitor 1.00 s after the switch is closed is 0 V

Step-by-step explanation:

The given parameters are

The length of the graphite pencil, L = 5.00 cm

The diameter of the graphite, D = 0.05 mm

The resistivity of the graphite, ρ = 1.38 × 10⁻⁵ Ω/m

The capacitance of the capacitor, C = 10.0 mF

The voltage of the power source, V = 0.50-V

(a) The RC time constant of the circuit, τ, is given as follows;

τ = R × C

Where;

R = The resistance of the graphite = L × ρ

C = The capacitance of the capacitor

∴ R = 5.00 cm × 1.38 × 10⁻⁵ Ω/m = 6.9 × 10⁻⁷ Ω

RC time constant of the circuit, τ = 6.9 × 10⁻⁷ Ω × 10.0 mF = 6.9 × 10⁻⁶ ms

RC time constant of the circuit, τ = 6.9 × 10⁻⁶ ms

(b) The potential drop after t = 1.00 s is given as follows;

`i = (V)/(R) \cdot e^{-(t)/(R\cdot C) }`

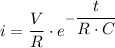
Where;

I = The current in the circuit

V = The voltage in the circuit = 0.50 V

R = resistance in the circuit = 6.9 × 10⁻⁷ Ω

C = The series capacitance = 10.0 mF

t = The time taken = 1.00 s

Plugging in the variable values, gives;

`I = (0.5)/(6.9 * 10^(-7)) \cdot e^{-(1.00)/(6.9 * 10^(-7)* 10.0 \ mF) } = 0`

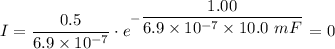
V(1) = I·R = 0 × R = 0

The potential drop across the capacitor 1.00 s after the switch is closed, V(1) = 0 V