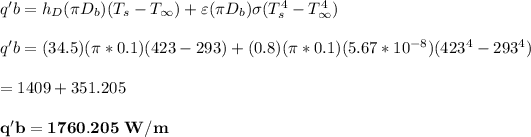Answer:
Heat loss per unit length = 642.358 W/m
The heat loss per unit length on a breezy day during 8 m/s speed is = 1760.205 W/m
Step-by-step explanation:
From the information given:
Diameter D
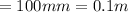
Surface emissivity ε = 0.8
Temperature of steam
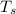 = 150° C = 423K
= 150° C = 423K
Atmospheric air temperature
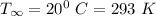
Velocity of wind V = 8 m/s
To calculate average film temperature:
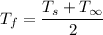
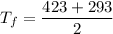
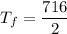
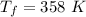
To calculate volume expansion coefficient
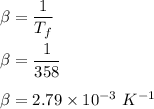
From the table of "Thermophysical properties of gases at atmospheric pressure" relating to 358 K of average film temperature; the following data are obtained;
Kinematic viscosity (v) = 21.7984 × 10⁻⁶ m²/s
Thermal conductivity k = 30.608 × 10⁻³ W/m.K
Thermal diffusivity ∝ = 31.244 × 10⁻⁶ m²/s
Prandtl no. Pr = 0.698
Rayleigh No. for the steam line is determined as follows:
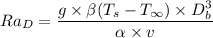
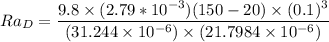
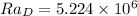
The average Nusselt number is:
![Nu_D = \Big \{ 0.60 + (0.387(Ra_D)^(1/6))/([ 1+ (0.559/Pr)^(9/16)]^(8/27)) \Big \}^2](https://img.qammunity.org/2022/formulas/physics/college/3j6afk9oba2uil2aq05qptdkfe6tubyruq.png)
![Nu_D = \Big \{ 0.60 + (0.387(5.224* 10^6)^(1/6))/([ 1+ (0.559/0.698)^(9/16)]^(8/27)) \Big \}^2](https://img.qammunity.org/2022/formulas/physics/college/adml1jj4yll39e64ddq0c3rwsz2kn4levy.png)
![Nu_D = \Big \{ 0.60 + (5.0977)/([ 1.8826]^(8/27))\Big \}^2](https://img.qammunity.org/2022/formulas/physics/college/refgt3fum2z5z7cah5kwjw7yhi04ppij7r.png)
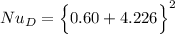
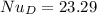
However, for the heat transfer coefficient; we have:
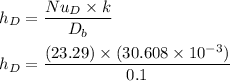
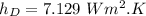
Hence, Stefan-Boltzmann constant
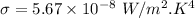
Now;
To determine the heat loss using the formula:
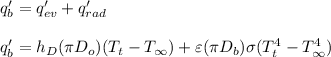
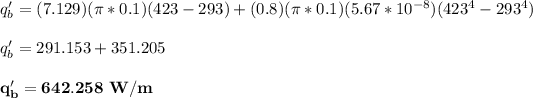
Now; here we need to determine the Reynold no and the average Nusselt number:
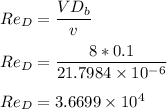
However, to determine the avg. Nusselt no by using Churchill-Bernstein correlation, we have;
![Nu_D = 0.3 + (0.62 * Re_D^(1/2)* Pr^(1/3))/([1+(0.4/Pr)^(2/3)]^(1/4)) [1+ ((Re_D)/(282000))^(5/8)]^(4/5)](https://img.qammunity.org/2022/formulas/physics/college/sngvyhn4uflmr67rlotgtqu83gg6mjkn9i.png)
![Nu_D = 0.3 + (0.62 * (3.6699*10^4)^(1/2)* (0.698)^(1/3))/([1+(0.4/0.698)^(2/3)]^(1/4)) [1+ ((3.669*10^4)/(282000))^(5/8)]^(4/5)](https://img.qammunity.org/2022/formulas/physics/college/aam3cvak5czn18sm08exc5egp8omibpzgv.png)
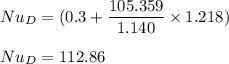
SO, the heat transfer coefficient for forced convection is determined as follows afterward:
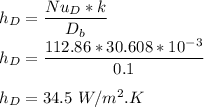
Finally; The heat loss per unit length on a breezy day during 8 m/s speed is: