Question

Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Then use your calculator to evaluate the integral correct to five decimal places. x2 4y2

Answer 1

The integral of the volume is:

`V = 32\pi\int\limits^1_0 {√((1 - y^2)) \, dy`

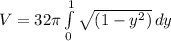
The result is:
`V = 78.97731`

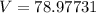
Explanation:

Given

Curve:
`x^2 + 4y^2 = 4`

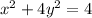
About line
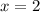`x = 2` --- Missing information

Required

Set up an integral for the volume

`x^2 + 4y^2 = 4`

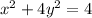
Make x^2 the subject

`x^2 = 4 - 4y^2`

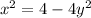
Square both sides

`x = \sqrt{(4 - 4y^2)`

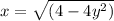
Factor out 4

`x = \sqrt{4(1 - y^2)`

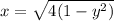
Split

`x = √(4) * \sqrt{(1 - y^2)`

`x = \±2 * \sqrt{(1 - y^2)`

`x = \±2 \sqrt{(1 - y^2)`

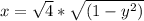
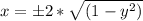
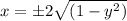
Split

`x_1 = -2 √((1 - y^2))\ and\ x_2 = 2 √((1 - y^2))`

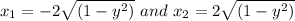
Rotate about x = 2 implies that:

`r = 2 - x`

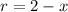
So:

`r_1 = 2 - (-2 √((1 - y^2)))`

`r_1 = 2 +2 √((1 - y^2))`

`r_2 = 2 - 2 √((1 - y^2))`

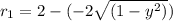
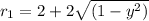
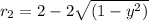
Using washer method along the y-axis i.e. integral from 0 to 1.

We have:

`V = 2\pi\int\limits^1_0 {(r_1^2 - r_2^2)} \, dy`

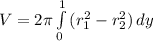
Substitute values for r1 and r2

`V = 2\pi\int\limits^1_0 {(( 2 +2 √((1 - y^2)))^2 - ( 2 -2 √((1 - y^2)))^2)} \, dy`

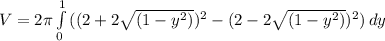
Evaluate the squares

`V = 2\pi\int\limits^1_0 {(4 +8 √((1 - y^2)) + 4(1 - y^2)) - (4 -8 √((1 - y^2)) + 4(1 - y^2))} \, dy`

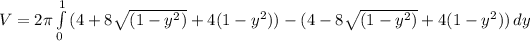
Remove brackets and collect like terms

`V = 2\pi\int\limits^1_0 {4 - 4 + 8√((1 - y^2)) +8 √((1 - y^2))+ 4(1 - y^2) - 4(1 - y^2)} \, dy`

`V = 2\pi\int\limits^1_0 { 16√((1 - y^2)) \, dy`

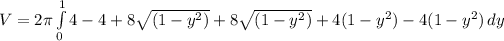
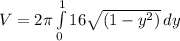
Rewrite as:

`V = 16* 2\pi\int\limits^1_0 {√((1 - y^2)) \, dy`

`V = 32\pi\int\limits^1_0 {√((1 - y^2)) \, dy`

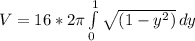
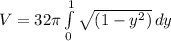
Using the calculator:

`\int\limits^1_0 {√((1 - y^2)) \, dy = (\pi)/(4)`

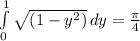
So:

`V = 32\pi\int\limits^1_0 {√((1 - y^2)) \, dy`

`V = 32\pi * (\pi)/(4)`

`V =(32\pi^2)/(4)`

`V =8\pi^2`

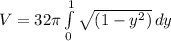
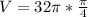
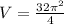
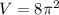
Take:

`\pi = 3.142`

`V = 8* 3.142^2`

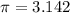
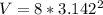
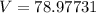`V = 78.97731` --- approximated