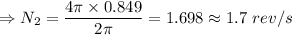Answer:1.7 rev/s
Step-by-step explanation:
Given
Frequency of wheel
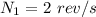
angular speed
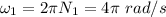
mass of wheel
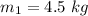
diameter of wheel
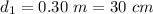
radius of wheel
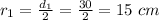
mass of clay

the radius of the chunk of clay
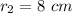
Moment of inertia of Wheel

Combined moment of inertia of wheel and clay chunk
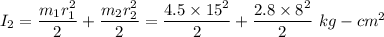
Conserving angular momentum
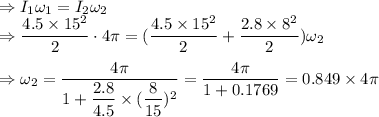
Common frequency of wheel and chunk of clay is