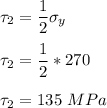Question

Construct the plane-stress yield envelopes in a principle stress space for both the Tresca and the von Mises yield theories using your calculated value of the yield strength to scale the envelopes. Indicate the two equivalent load paths corresponding to pure shear on the yield envelopes. Calculate the shear yield strength of Al 6061-T6 aluminum predicted by the above theories.

Answer 1

Step-by-step explanation:

The missing part of the question is attached in the diagram below, the second diagram shows the schematic view of the stress-strain curve and the plane stress.

From the given information:

The elastic modulus is:

`E = (\sigma)/(\varepsilon) \\ \\ E = (150 \ MPa)/(0.0217) \\ \\ E = 69.124 \ GPa`

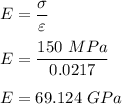
Hence, suppose 0.2% offset cuts the stress-strain curve at a designated point A from the image attached below, then the yield strength relating to the stress axis from the curve will be
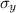`\sigma_y` = 270 MPa.

The shear yield strength by using von Mises criteria is estimated as;

`\tau_1 = (√(2))/(3)\sigma_y \\ \\ \tau_1 = (√(2))/(3)*270 \\ \\ \tau_1 = 127.28 \ MPa`

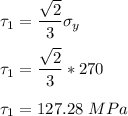
The shear yield strength by using Tresca criteria is:

`\tau_2 = (1)/(2)\sigma_y \\ \\ \tau_2= (1)/(2)*270 \\ \\ \tau_2 = 135 \ MPa`