Question

What is the perimeter of the triangle below?

a. 14.7 units
b. 48 units
c. 24 units
d. 16.7 units

Answer 1

B) 48 units
Dkdjddijdidjkddjidjdjdjdjfj

Answer 2

The perimeter of the triangle is approximately 16.73 ft. Hence, the correct answer is the option d.16.7 units.

To find the perimeter of the right-angled triangle, we need to know the lengths of all three sides.

Given that the triangle has two angles of 45 degrees each and one right angle, we can determine that it is an isosceles right triangle, where the two legs are congruent.

Let's label the sides:
- Side opposite the right angle: Hypotenuse (r)
- Two congruent legs: Side 1 (4.9 ft) and Side 2 (4.9 ft)

Since the two legs are congruent, we know that Side 1 = Side 2 = 4.9 ft.

To find the hypotenuse (r), we can use the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

In this case, it becomes:

`r^2 = (4.9 ft)^2 + (4.9 ft)^2`

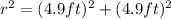
Simplifying the equation, we get:

`r^2 = 24.01 ft^2 + 24.01 ft^2`

`r^2 = 48.02 ft^2`

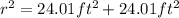
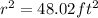
Taking the square root of both sides, we find:
r ≈ 6.93 ft

Now that we know the lengths of all three sides, we can calculate the perimeter by summing the lengths of the sides:
Perimeter = Side 1 + Side 2 + Hypotenuse
Perimeter = 4.9 ft + 4.9 ft + 6.93 ft
Perimeter ≈ 16.73 ft