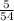Answer:
a) P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) =

b) P( the sum of both dice adding up to 4) =
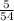
Explanation:
Given - You roll two six-sided dice. Die 1 is fair. Die 2 is unfair such that the probability of rolling an odd number is
 and the probability of rolling an even number is
and the probability of rolling an even number is
 , though the probability rolling of each odd number is the same, and the probability of rolling each even number is the same.
, though the probability rolling of each odd number is the same, and the probability of rolling each even number is the same.
To find - What is the probability of:
a) rolling a number less than 4 on Die 1 and rolling a 5 on Die 2.
b) the sum of both dice adding up to 4.
Proof -
The sample space , S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
Now,
Given that , Dice 1 is fair
⇒P₁(1) = P₁(2) = P₁(3) = P₁(4) = P₁(5) = P₁(6) =
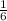
Also, Given Dice 2 is unfair
⇒P₂(1) = P₂(3) = P₂(5) =
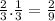
P₂(2) = P₂(4) = P₂(6) =
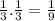
Now,
a)
P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) = P₁(1)P₂(5) + P₁(2)P₂(5) + P₁(3)P₂(5)
= P₂(5) [ P₁(1) + P₁(2) + P₁(3) ]
=
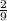 [
[
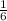 +
+
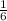 +
+
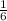 ] =
] =
![(2)/(9)[ (3)/(6)]\\](https://img.qammunity.org/2022/formulas/mathematics/college/5rnhwqlfktl8spw99o2xvhs2e06qtdy842.png) =
=

⇒P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) =

b)
P( the sum of both dice adding up to 4) = P₁(1)P₂(3) + P₁(2)P₂(2) + P₁(3)P₂(1)
=
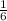 ×
×
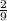 +
+
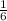 ×
×
 +
+
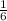 ×
×
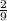 =
=
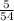
⇒P( the sum of both dice adding up to 4) =