Final answer:
The height of the airplane above the ground, with an angle of elevation of 50 degrees and observed at a horizontal distance of 12 km, can be found using the tangent function. The height is approximately 14.302 kilometers.
Step-by-step explanation:
To find the height of the airplane above the ground, we can use trigonometric ratios, specifically the tangent of the angle of elevation. The tangent of an angle in a right triangle is the ratio of the side opposite to the angle (the height of the airplane, in our case) to the side adjacent to the angle (the distance from the point of observation to the airplane).
Let's denote the height of the airplane as h, and the distance from the observation point to the airplane as 12 km (horizontal distance). The angle of elevation is given as 50 degrees. We may write:
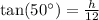
From this, we can solve for h:
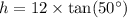
After calculating the tangent of 50 degrees and multiplying by 12, we find the height h:
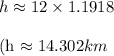
The height of the airplane above the ground is approximately 14.302 kilometers.