Answer:
The claim is valid for 98% confidence interval. A further explanation is described below.
Explanation:
The given values are:
Sample size,
n = 38
Sample mean,
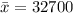
Population standard deviation,
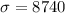
For 98% confidence interval,
Mean =
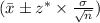
On substituting the given values, we get
=
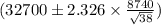
=
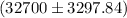
=
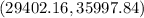
Thus the above is the appropriate solution.