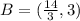Question

Point C open parentheses 4 comma space 2 close parentheses divides the line segment joining points A open parentheses 2 comma space minus 1 close parentheses and B open parentheses x comma space y close parentheses such that A C : C B equal 3 : 1. What are the coordinates of point B?

Answer 1

Question:

Point C (4,2) divides the line segment joining points A(2,-1) and B(x, y) such that AC: CB = 3:1.

What are the coordinates of point B?

Answer:

`B = ((14)/(3),3)`

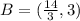
Explanation:

Given

`C = (4,2)`

`A = (2,-1)`

`AC : CB = 3 : 1`

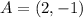
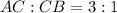
Required

Find the coordinates of B

Coordinates of a line segment is calculated using:

`(x,y) = ((mx_2+nx_1)/(n+m), (my_2 + ny_1)/(n+m))`

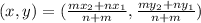
In this case:

`(x,y) = (4,2)`

`AC:CB = m : n = 3:1`

`A = (2,-1)` ---
`(x_1,y_1)`

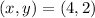
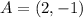The equation becomes

`(4,2) = ((3x_2+2)/(1+3), (3y_2 - 1)/(1+3))`

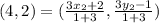
So, the coordinates of B is:
`(x_2,y_2)`

Solving further

`(4,2) = ((3x_2+2)/(4), (3y_2 - 1)/(4))`

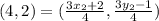
Multiply through by 4

`4 * (4,2) = ((3x_2+2)/(4), (3y_2 - 1)/(4)) * 4`

`(16,8) = (3x_2+2, 3y_2 - 1)`

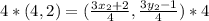
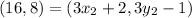
By comparison:

`3x_2 + 2 = 16`

`3y_2 - 1 = 8`

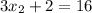
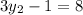
So:

`3x_2 + 2 = 16`

`3x_2 = 16 - 2`

`3x_2 = 14`

`x_2 = (14)/(3)`

`3y_2 - 1 = 8`

`3y_2 = 8+1`

`3y_2 = 9`

`y_2 = 3`

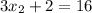
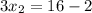
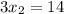
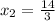
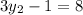
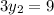
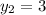
The coordinates of B is:

`B = ((14)/(3),3)`