Answer:
(a) Dan’s supply function S(P) can be stated as follows:
S(P)= 0 If P<4.
And S(P) = 20P- 80 If P≥4
(b) Dan’s supply function S(P) can be stated as follows:
S(P)= 0 If P<5.
And S(P) = 20P- 80 If P≥5.
Step-by-step explanation:
Note that the equations given in the question can be correctly stated as follows:
C(Q) = 4Q + (Q^2/40) .................. (1)
MC = 4 + (Q/20) ............................ (2)
Therefore, we can now proceed as follows:
(a) What is Dan’s supply function?
The upward portion of the MC curve is the supply function of Dan.
Equating equation (2) to P, we have:
P = 4+ (Q/20)
P- 4 = Q/20
Q = 20P -80
The shutdown rule is that P > AVCmin
AVC = C(Q) / Q .................. (3)
Substituting equation (1) into (3), we have:
AVC = ( 4Q + Q^2/40)/ Q
AVC = 4 + (Q/40) ............... (4)
Since MC cuts the AVC at its minimum, equations (2) and (4) are then equated to solve Q which is the output level at which AVC is minimum as follows:
4 + (Q/20) = 4 + (Q/40)
(Q/20) - (Q/40) = 4 - 4
(Q/20) - (Q/40) = 0
Q = 0
Substituting Q = 0 into equation (4), we have:
AVCmin = 4+ (0/40)
AVCmin = 4
This implies that Dan will produce at any price ≥ $4.
Therefore, Dan’s supply function S(P) can be stated as follows:
S(P)= 0 If P<4.
And S(P) = 20P- 80 If P≥ 4.
(b) What is Dan’s supply function if he has an avoidable fixed cost of $10?
Since there is now a fixed cost, equation (1) becomes:
C(Q) = 4Q + (Q^2/40) + 10 ................. (5)
And the average cost (AC) will be as follows:
AC = (4Q + (Q2/40) + 10)/Q
AC = 4 + (Q/40) + (10/Q) .................... (6)
Since AC = MC when AC at its minimum, equations (2) and (6) are therefore equated to solve for Q as follows:
4 + (Q/40) + (10/Q) = 4 + (Q/20)
(Q/40) + (10/Q) = (Q/20)
Q = 20
Divide through by Q, we have:
(1/40) + (10/Q^2) = (1/20)
10/Q^2 = (1/20) - (1/40)
10/Q^2 = 0.05 - 0.025
10/Q^2 = 0.025
Q^2 = 10 / 0.025
Q^2 = 400
Q =
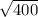
Q = 20
Substituting Q = 20 into equation (6), we have:
AC = 4 + (20/40) + (10/20)
AC = $5
This implies that Dan will produce at any price ≥ $5.
Therefore, Dan’s supply function S(P) can be stated as follows:
S(P)= 0 If P<5.
And S(P) = 20P- 80 If P≥ 5