Answer:
The minimum cost is $17.30c
Explanation:
Given
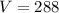 --- Volume
--- Volume
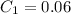 --- cost of wall paint
--- cost of wall paint
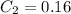 ---cost of ceiling paint
---cost of ceiling paint
Required
Minimum cost of paint
The volume is calculated as:
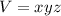
Substitute 288 for V
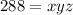
Make z the subject
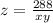
The surface area is calculated as:

Because xy represent the dimension of the ceiling and the opposite of the ceiling (the floor) will not be painted. Hence, it does not require a coefficient of 2
The cost is:
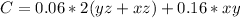
Substitute
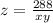
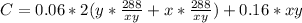

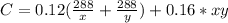
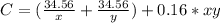
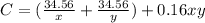
Differentiate w.r.t x and y
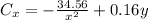
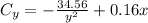
By comparison:

Set them equal to 0
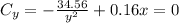
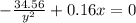
Substitute x for y
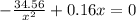
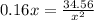
Cross multiply
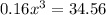
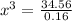
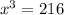
Take the cube root of both sides
![x = \sqrt[3]{216}](https://img.qammunity.org/2022/formulas/mathematics/college/s908h8pdad4ds3vsc8w5gmlxofqk4oqqv9.png)
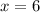
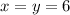
Substitute 6 for x and for y in
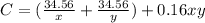
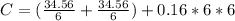
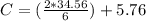
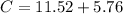
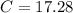
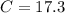 --- approximated
--- approximated