Question

A 52 kg and a 95 kg skydiver jump from an airplane at an altitude of 4750 m, both falling in the pike position. Assume all values are accurate to three significant digits. (Assume that the density of air is 1.21 kg/m3 and the drag coefficient of a skydiver in a pike position is 0.7.) If each skydiver has a frontal area of 0.14 m2, calculate their terminal velocities (in m/s). 52 kg skydiver m/s 95 kg skydiver m/s How long will it take (in s) for each skydiver to reach the ground (assuming the time to reach terminal velocity is small)

Answer 1

Answer: 52 kg skydiver: 9.09 m/s and 522.55 s

95 kg skydiver: 12.3 m/s and 386.2 s

Step-by-step explanation: Drag Force is an opposite force when an object is moving in a fluid.

For skydivers, when falling through the air, the forces acting on it are gravitational and drag forces. At a certain point, drag force equals gravitational force, which is constant on any part of the planet, producing a net force that is zero. Since there is no net force, there is no acceleration and, consequently, velocity is constant. When that happens, the person reached the Terminal Velocity.

Drag Force and Velocity are proportional to the squared speed. So, terminal velocity is given by:

`F_(G)=F_(D)`

`mg=(1)/(2)C \rho Av_(T)^(2)`

`v_(T)=\sqrt{(2mg)/(\rho CA) }`

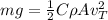
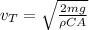
where

m is mass in kg

g is acceleration due to gravitational force in m/s²

ρ is density of the fluid in kg/m³

C is drag coefficient

A is area of the object in the fluid in m²

Calculating:

The 52kg skydiver has terminal velocity of:

`v_(T)=\sqrt{(2(52)(9.8))/((1.21)(0.7)(0.14)) }`

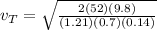
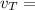`v_(T)=` 9.09

The 95kg skydiver's terminal velocity is

`v_(T)=\sqrt{(2(95)(9.8))/((1.21)(0.7)(0.14)) }`

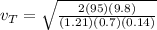
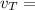`v_(T)=` 12.3

The 52 kg and 95kg skydivers' terminal velocity are 9.09m/s and 12.3m/s, respectively.

The time each one will reach the floor will be:

52 kg at 9.09 m/s:

`t=(4750)/(9.09)`

t = 522.5

95 kg at 12.3 m/s:

`t=(4750)/(12.3)`

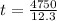
t = 386.2

The 52 kg and 95kg skydivers' time to reach the floor are 522.5 s and 386.2 s, respectively.