Question

State whether the triangles are similar. If so, write

or theorem

you used.

a similarity statement and the postulate

Answer 1

Both triangles are similar by SAS

Explanation:

See attachment for triangles

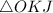`\triangle OKJ` and
`\triangle ONM`

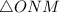
From the attachment:

`OK = 3; OJ = 30; KN = 1; JM = 3`

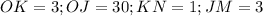
Calculate the lengths of ON and OM

`ON=OK+KN=3+1= 4`

`OM = OJ + JM = 30 + 10 = 40`

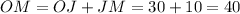
To determine if both triangles are similar or not, we make use of the following equivalent ratios

`OK : OJ = ON : OM`

`3 : 30 = 4 : 40`

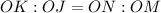
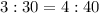
Divide the first ratio by 3 and the second by 4

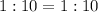`1:10 = 1 : 10` --- This implies that both triangles have 2 similar sides

From the attachment,

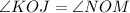`\angle KOJ = \angle NOM` ---- similar angles

Since the two triangles have 2 similar sides and a similar angle, then both triangles are similar by SAS